| (問題1) |
直線上をともに毎秒2cmの速さで向かい合って移動する直角三角形A,Bが、図1の位置から図2の位置になるのは何秒後ですか。 → 解答 |
 |
| (問題2) |
図のように直角三角形ABCをA'B'C'の位置まで平行移動したとき、台形A'PCC'の面積は140cm2になりました。何cm平行移動したか答えなさい。 → 解答 |
 |
| (問題3) |
上底4cm、下底10cmの台形ABCDを図のように平行移動したところ、黒くぬった部分の面積は27cm2になりました。台形ABCDの高さを求めなさい。 → 解答 |
 |
| (問題4) |
図のように、1辺が10cmの正方形ABCDとCDを直径とする半円があります。半円の直径CDをABの方向に2cm平行移動してC'D'としたとき、黒くぬった部分の面積を求めなさい。円周率は3.14とします。 → 解答 |
 |
| (問題5) |
図のように直角三角形ABCが毎秒4cmの速さで矢印の方向に平行移動します。5秒後に直角三角形ABCと正方形DEFGが重なる部分の面積を求めなさい。 → 解答 |
 |
| (問題6) |
対角線の長さが8cmの正方形を1つの頂点を中心に図のように45°回転させました。黒くぬった部分の面積を求めなさい。円周率は3.14とします。 → 解答 |
 |
| (問題7) |
図のように、直角三角形ABCを頂点Aを中心に60°回転させました。黒くぬった部分の面積を求めなさい。円周率は、3.14とします。 → 解答 |
 |
| (問題8) |
面積が100cm2の半円を図のように45°回転させました。黒くぬった部分の面積を求めなさい。 → 解答 |
 |
| (問題9) |
図のような直角二等辺三角形OABを頂点Oを中心に1回転させたとき、辺ABが通る部分の面積を求めなさい。円周率は3.14とします。 → 解答 |
 |
| (問題10) |
図のような直角二等辺三角形OABを直線上をすべらないように転がして辺OAが直線上にもどったとき、点Oが通ったあとの線の長さを求めなさい。円周率は3.14とします。 → 解答 |
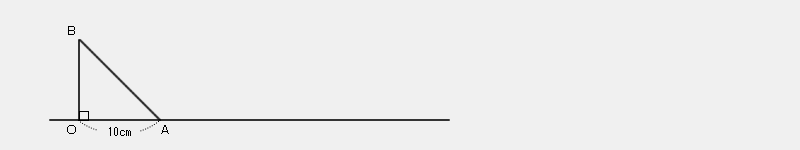 |
| (問題11) |
たて24cm、よこ36cmの長方形Aの内側の辺にそって、半径3cmの円Bが1周します。円の通った部分の面積を求めなさい。円周率は3.14とします。 → 解答 |
 |
| (問題12) |
1辺8cmの正三角形の外側の辺にそって直径4cmの円が1周します。円が通った部分の面積を求めなさい。円周率は3.14とします。 → 解答 |
 |
 |
 |
| |
|
 |
| (問題14) |
直径8cmの円Aのまわりを直径2cmの円Bが、円周を接しながらすべらないように周回します。円Bは1周する間に何回転しますか。円周率は3.14とします。 → 解答 |
 |
| (問題15) |
直径12cmの円Aの内側を直径4cmの円Bが、円周を接しながらすべらないように周回します。円Bは1周する間に何回転しますか。円周率は3.14とします。 → 解答 |
 |
 |
|
 |
 |
|
 |
 |
 |
| |
|
 |
 |
|
 |
 |
|
 |
| (問題21) |
図のような長方形ABCDがあり、点P,Qは点Aを同時に出発し、矢印の方向に進みます。点Pが毎秒5cm、点Qが毎秒6cmで進むとき、85秒後にできる三角形APQの面積を求めなさい。 → 解答 |
 |
| (問題22) |
図のような平行四辺形ABCDの辺上を点Pは頂点Aから毎秒5cmの速さで、点Qは頂点Bから毎秒3cmの速さで同時に矢印の方向に出発します。点P,Qを結ぶ直線が平行四辺形の面積を最初に2等分するのは、出発してから何秒後ですか。 → 解答 |
 |
| (問題23) |
図のような1辺16cmの正三角形ABCの辺上を3点P,Q,Rが、それぞれ頂点A,B,Cから毎秒4cm,毎秒6cm,毎秒12cmの速さで矢印の方向に同時に出発します。3点が、はじめて同時に出発点に戻るのは、出発してから何秒後ですか。 → 解答 |
 |
| (問題24) |
図のような1辺16cmの正方形ABCDがあり、点E,Fは、それぞれ辺AB,CDのまん中の点です。点Pは、点Bから出発して辺BC上を毎秒2cmの速さで動きます。三角形ABPと長方形AEFDが重なる部分の面積をSとすると、点Pが出発してから3秒後から5秒後の間に面積Sは何cm2大きくなりますか。 → 解答 |
 |
| (問題25) |
図のように1辺が60cmの正三角形の形をした柱があり、その1つの頂点にあたる部分から長さ90cmのひもがついた首輪をはめられた犬がいます。この犬が行動できる範囲の面積を求めなさい。ただし、円周率は3.14、犬の大きさはなく、犬は柱の内部には入れないものとします。 → 解答 |
 |